Rather than just generating a realistic output with our GAN, in many cases we’d like to generate a plausible output given some input. In fact, I think that most of the big applications for GANs other than for the sake of cool demonstrations fall in this category, one way or another. Such GANs are called conditional GANs (CGANs), as they generate a distribution of outputs conditioned to a given input. The extension of GANs to make them conditional is quite straightforward and existing GANs can be adapted fairly easily into conditional designs.
The Theory
In the regular GAN, the generator receives a noise input and outputs an artificial sample, while the discriminator input is a sample and its output is related to whether the discriminator considers the sample a real or generated one. In the CGAN, we give the generator a conditioning variable as well as the noise. We also pass this variable to the discriminator in addition to the sample, and the task of discriminator is now to determine if the sample and the condition are a plausible pair.
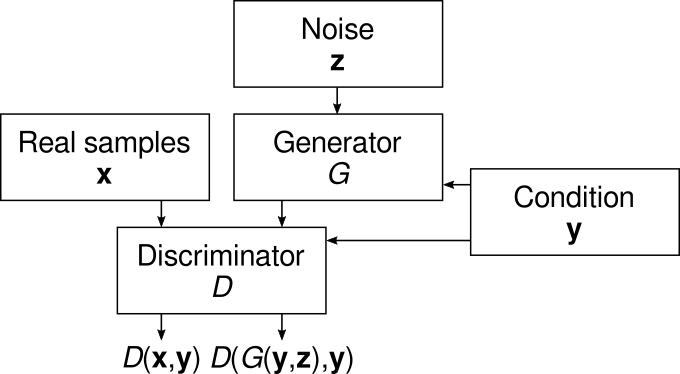
Using the same notation as in the first part and denoting our condition as \( \mathbf{y} \), the discriminator objective becomes \[ \min_D E_{\mathbf{x},\mathbf{y},\mathbf{z}} [ L_D(D(\mathbf{x},\mathbf{y}),D(G(\mathbf{y},\mathbf{z}),\mathbf{y})) ] \] while the generator objective is \[ \min_G E_{\mathbf{y},\mathbf{z}} [ L_G(D(G(\mathbf{y},\mathbf{z}))) ] . \] Comparing this to the objectives of the basic GAN, we see that the only changes we need to make to the implementation is to add the condition inputs and processing to the discriminator and the generator, and to sample input-output pairs (just like we would when training a predictive model). We can use the same losses and GAN training techniques as we did for regular GANs, which makes it simple to train, say, Wasserstein GANs with conditions.
The Code
In this example, we work with the MNIST dataset using the digit label as the condition and see if our conditional GAN learns to generate examples for each label separately. We represent the label with a one-hot vector of length 10 (since there are 10 different digits). But we could also use a more complex condition — for example, an entire image — as the condition, and would just have to modify the network to accept and process such inputs.
For simplicity, we use the basic GAN architecture from Part 1 as the basis of the implementation. First, we modify the generator and the discriminator to include the condition inputs. There is more than one way to do this, and we’ll use different approaches for the generator and the discriminator to demonstrate two of them. For the generator, we can simply concatenate the condition and noise inputs, and leave the network structure otherwise unchanged except for making the upsampling layers a bit wider:
def cgan_gen(img_shape=(32,32,1), noise_dim=64):
# ...
cond_in = Input(shape=(10,), name="cond_in")
noise_in = Input(shape=(noise_dim,), name="noise_in")
inputs = Concatenate()([cond_in,noise_in])
# ...
x = up_block(256)(x)
x = up_block(128)(x)
# ...
return Model(inputs=[cond_in,noise_in], outputs=img_out)
For the discriminator, we have to make a few more changes because one of the inputs of the discriminator is an image and the other is a plain vector. We extract the features from the image using convolutional layers, flatten them and pass them to a fully connected layer. In another branch, we process the condition with a couple of fully connected layers, and then multiply the image feature vector with this.
def cgan_disc(img_shape=(32,32,1)):
# ...
image_in = Input(shape=img_shape, name="sample_in")
cond_in = Input(shape=(10,), name="cond_in")
x = conv_block(64, strides=1)(image_in)
x = conv_block(128)(x)
x = conv_block(256)(x)
x = Flatten()(x)
x = Dense(256)(x)
c = Dense(256)(cond_in)
c = LeakyReLU(0.2)(c)
c = Dense(256)(c)
x = Multiply()([x,c])
x = Dense(256)(x)
x = LeakyReLU(0.2)(x)
x = Dense(256)(x)
x = LeakyReLU(0.2)(x)
disc_out = Dense(1, activation="sigmoid")(x)
model = Model(inputs=[image_in,cond_in], outputs=disc_out)
return model
In principle, we could just replace the Multiply layer with a Concatenate layer to use a similar technique as we did in the generator. Spoiler alert: this doesn’t work! I found that if I use Concatenate, the GAN doesn’t learn to properly condition the outputs to the input, generating random digits instead similar to the vanilla GAN. It turns out that the multiplication technique is quite powerful in CGANs as it allows us to modulate the behavior of one layer with another. Then again, sometimes it just leads to horrible instability. Such is life when training GANs.
Results
Here are the results of training the CGAN with one label on each column:

The CGAN clearly differentiates between the number labels and still generates a decent amount of diversity within each digit. The results are quite a bit better than with the unconditional GAN. This is not uncommon in my experience: The additional input produces a useful constraint that helps convergence.